Question

Determine if the point ( -15/8, -4) lies on the line 4(y+3) = -4/3x - 13/2

Answer 1

start by writting the line in the slope-intercept form

`\begin{gathered} 4(y-3)=-(4)/(3)x-(13)/(2) \\ 4y-12=-(4)/(3)x-(13)/(2) \\ 4y=-(4)/(3)x-(13)/(2)+12 \\ 4y=-(4)/(3)x+(11)/(2) \\ y=-(1)/(3)x+(11)/(8) \end{gathered}`

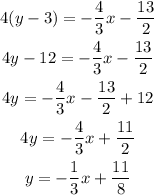
replace the coordinate x of the point to see if the point lies on the line, if the coordinate y is equal to the result then the point lies on the line

`\begin{gathered} y=-(1)/(3)(-(15)/(8))+(11)/(8) \\ y=(5)/(8)+(11)/(8) \\ y=2 \end{gathered}`

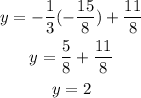
Since 2 is different from -4 then the point does not lie on the line.