Question

Find the intercept and domain, and perform the symmetry test on each of the following ellipsesx^2 + 4y^2 = 4

Answer 1

The given equation of the ellipse is:

`x^2+4y^2\text{ = 4}`

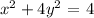
To find the x intercept, let y = 0

`\begin{gathered} x^2+4(0)^2\text{ = 4} \\ x\text{ = }\sqrt[]{4} \\ x\text{ = }\pm2 \\ x-\text{intercept = (}\pm2,\text{ 0)} \end{gathered}`

For the y-intercept, let x = 0

`\begin{gathered} 0^2+4y^2=4 \\ y^2\text{ = }(4)/(4) \\ y\text{ = }\sqrt[]{1} \\ y\text{ = }\pm1 \\ y-\text{intercept = (0, }\pm1) \end{gathered}`

For an ellipse of the form:

`\begin{gathered} (x^2)/(a^2)+(y^2)/(b^2)=1 \\ \text{The x-domain is from -a and a} \\ \text{The y-domain is from -b and b} \end{gathered}`

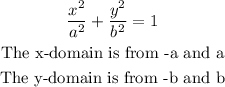
The given equation is:

`\begin{gathered} x^2+4y^2=\text{ 4} \\ \text{Divide through by 4} \\ (x^2)/(4)+(y^2)/(1)=(4)/(4) \\ (x^2)/(4)+(y^2)/(1)=\text{ 1} \end{gathered}`
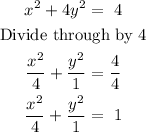
`\begin{gathered} a^2\text{ = 4} \\ a\text{ = }\sqrt[]{4} \\ a\text{ = -2, 2} \\ b^2\text{ = 1} \\ b\text{ = }\sqrt[]{1} \\ b\text{ = -1, 1} \end{gathered}`

The x-domain = (-2, 2)

The y-domain = (-1, 1)

Symmetry test:

For the equation to be symmetriacal to the x-axis, y → -y

`\begin{gathered} x^2+4y^2\text{ = 4} \\ y^2\text{ = 1 - }(x^2)/(4)\ldots\ldots\text{.}(1) \\ \text{Let y = -y} \\ (-y)^2\text{ = 1 - }(x^2)/(4) \\ y^2\text{ = 1 - }(x^2)/(4)\ldots\ldots\text{.}\mathrm{}(2) \\ \end{gathered}`

Because (1) matches with (2), the equation is symmetrical to the x-axis

For the equation to be symmetrical to the y-axis, x → -x

`\begin{gathered} x^2+4y^2\text{ = 4}\ldots..(1) \\ \text{Let x = -x} \\ (-x)^2+4y^2\text{ = 4} \\ x^2+4y^2\text{ = 4}\ldots.(2) \end{gathered}`

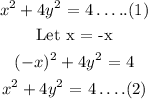
Since (1) matches with (2), the equation is symmetrical to the y-axis

For the equation to be symmetrical to the origin, x→-x, y→-y

`\begin{gathered} (-x)^2+4(-y)^2\text{ = 4} \\ x^2+4y^2\text{ = 4} \end{gathered}`

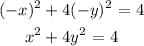
The equation is symmetrical to the origin

Therefore, according to the symmetry test, the equation given is symmetrical to the x-axis, y-axis, and the origin