Line equation
We know the line equation is expressed by
y = mx + b, where is m is its slope (how inclinated it is) and b is intercept with the y-axis.
Finding m
We find its inclination, its slope, m, by

Let's say
(x₁, y₁) = (-6, 5)
(x₂, y₂) = (-3, 3)
Then
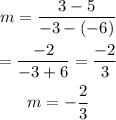
Then y = -(2/3)x + b,
Finding b
Since b is intercept with the y-axis, we know it intercepts y when x = 0
Using the equation we have found y = -(2/3)x + b, and replacing one point given by the question (x₂, y₂) = (-3, 3)
y = -(2/3)x + b
3 = -(2/3)(-3) + b
3 = -2 + b
3 + 2 = b
Then, b = 5
Therefore,
Answer, y = -(2/3)x + 5,