Question

Part A: Create a fourth-degree polynomial with two terms in standard form. How do you know it is in standard form? (5 points)Part B: Explain the closure property as it relates to subtraction of polynomials. Give an example. (5 points)

Answer 1

(a)f(x)=x⁴+3x²

Explanation:

Part A

A polynomial in the fourth degree is any polynomial in which the highest power is 4.

An example of a fourth-degree polynomial with two terms is given below:

`f(x)=x^4+3x^2`

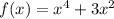
We know that this polynomial is in standard form since it is written in descending powers of x.

Part B

The closure property as it relates to the subtraction of polynomials tells us that when two polynomials are subtracted, one from the other, the result is always a polynomial.

Consider the polynomials, f(x) and g(x) below:

`\begin{gathered} f(x)=x^2-4 \\ g(x)=x^3+8 \end{gathered}`

Subtracting f(x) from g(x):

`\begin{gathered} g(x)-f(x)=\lbrack x^3+8\rbrack-\lbrack x^2-4\rbrack \\ =x^3+8-x^2+4 \\ =x^3-x^2+8-4 \\ =x^3-x^2+4 \end{gathered}`

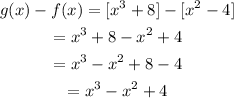
Observe that the result is also a polynomial, hence the closure property applies.