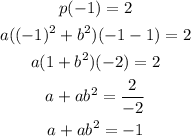Question

For each problem write an equation that describes the graphs shown below:

Answer 1

14) We have the graph of an odd-degree polynomial.

It has a real root at x = 1 and two imaginary (conjugate) roots.

We can write the polynomial in general terms as:

`p(x)=a(x^2+b^2)(x-c)`

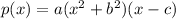
where x²+b² is the factor that correspond to the imaginary roots and (x-c) is the factor for the real root.

Parameter a is the cubic coefficient.

We know that the real root is x = 1, so c = 1.

We know can look at two known points in order to find a and b.

One point is (0,1) and the other is (-1,2).

Then, we can write for (0,1):

`\begin{gathered} p(0)=1 \\ a(0^2+b^2)(0-1)=1 \\ a\cdot b^2(-1)=1 \\ ab^2=-1 \end{gathered}`

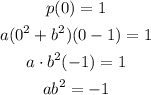
Now, if we use the point (-1,2), we get:

`\begin{gathered} p(-1)=2 \\ a((-1)^2+b^2)(-1-1)=2 \\ a(1+b^2)(-2)=2 \\ a+ab^2=(2)/(-2) \\ a+ab^2=-1 \end{gathered}`