Hello there. To solve this question, we'll have to remember some properties about dividing polynomials and finding rational expressions.
First, the monthly budget for the station is decided by the expression
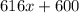
and the budget is split evenly between
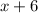
things, including the giveaway.
We know that during the giveaway, the prizes will be given to every
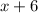
caller. The station usually receives
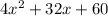
calls during the giveaway.
We want to determine a rational expression that models how much of the budget will go to the giveaway.
For this, we first have to determine how many
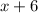
callers are in between the
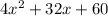
calls the station received.
Taking the ratio between calls and callers, we get:
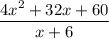
Notice we can rewrite the numerator as follows:
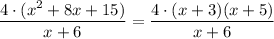
This expression, even though it cannot be simplified, gives us the number of callers of the type we're interested in.
Now, we have to find how much of the budget will go to the giveaway.
For this, we simply divide the budget by the number of callers we found before:
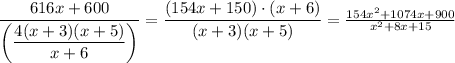
This is the rational expression that determines how much of the budget will go to the giveaway.