Question

Find the equation of the straight line which passes through the point (-2,7) and Perpendicular to the line -4y+2x=-3.

Answer 1

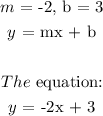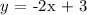
`y\text{ = -2x + 3}`Step-by-step explanation:

Given: point (-2, 7)

The given line is perpendicular to the line we are to find.

For a line to be perpendicular to another, the slope of one will be the negative reciprocal of the other slope.

`\begin{gathered} Equation\text{ of of the given line:} \\ -4y+2x=-3 \\ We\text{ need to write the equation in the form y = mx + b so as to get the slope} \\ -4y\text{ = -2x - 3} \\ (-4y)/(-4)\text{ = }(-2x)/(-4)-(3)/(-4) \\ y\text{ = }(1)/(2)x\text{ +}(3)/(4) \end{gathered}`
`\begin{gathered} from\text{ the equation y = }(1)/(2)x\text{ + }(3)/(4) \\ m\text{ = }slope\text{ = 1/2} \\ b\text{ = }y-intercept\text{ = 3/4} \end{gathered}`

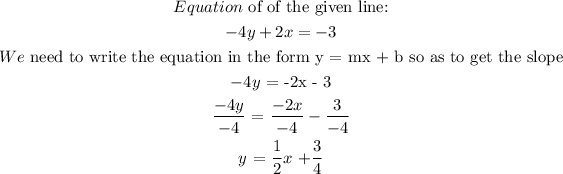
slope of the line perpendicular to the given line = negative reciprocal of the slope

slope = 1/2

reciprocal of the slope = 2/1 = 2

negative reciprocal = -2

2nd slope = -2

To get the equation of line with slope -2, we will use the point given:

`\begin{gathered} \left(-2,\text{ 7}\right):\text{ x = -2, y = 7} \\ y\text{ = mx + b} \\ 7\text{ = -2}\left(-2\right)\text{ + b} \\ 7\text{ = 4 + b} \\ 7\text{ - 4 = b} \\ b\text{ = 3} \end{gathered}`

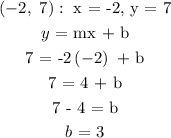
Th equation of line Perpendicular to the line -4y + 2x = -3 that passed through the point (-2, 7):

`\begin{gathered} m\text{ = -2, b = 3} \\ y\text{ = mx + b} \\ \\ The\text{ equation:} \\ y\text{ = -2x + 3} \end{gathered}`