The given function f(x) is:
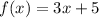
And the other given function g(x) is:
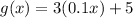
g(x) in comparison with f(x) has the next transformation:
1. g(x)=f(bx): g(x)=3(0.1x)+5. This is a horizontal stretch: the x-coordinates will change as:
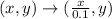
This is the graph of both functions:
The red-one is f(x) and the blue-one is g(x).
Then for example when the coordinates of f(x) are (1,8) for g(x) the coordinates will be:
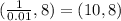
Then, the slope of f(x) has a greater value than the slope of g(x), since the change on the x-axis is bigger in the g(x) graph for the.