Solution:
From the amortization function:
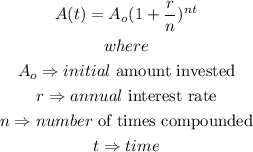
Given that $10,000 is invested at an annual rate of 5% compounded quarterly, this implies that
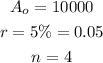
Thus, by substituting these values into the above equation, we have
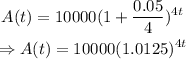
Given that the amount earned is double the initial amount invested, this implies that

Thus, we have
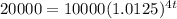
To solve for t,

Hence, it takes 13.94940762 years to double the amount invested.