The volume of a cone is given by the following formula:
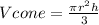
And the volume of a cylinder is given by the following formula:
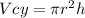
Where r is the radius and h is the height of the figure.
In this case, we are asked to find a set of dimensions for a cone so its volume equals the volume of a cylinder, then we can formulate the following expression:
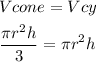
Let's assume that the radius of the cone equals 2, as the radius of the cylinder, then by replacing 4 for the height of the cylinder and 2 for the radius of both the cone and the cylinder, we get:
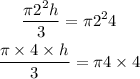
As you can see, we have 4π on both sides of this equation, by dividing the expression by 4π we can get rid of this factor, to get:
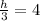
By multiplying both sides by 3, we get the height of the cone:

Then, a possible set of dimensions of a cone that has the same volume as the cylinder is a radius of 2 inches and a height of 12 inches.