For similar solids, the ratios of the two sides (R), two areas (A) and two volumes (V) are
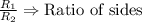
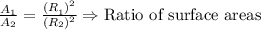
![\begin{gathered} (V_1)/(V_2)=((R_1)^3)/((R_2)^3) \\ 3\sqrt[]{(V_1)/(V_2)}=(R_1)/(R_2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/l0b86m8vdqdryma4fwy6y5w7ot35804leh.png)
Therefore, we can relate the volumes as follows:
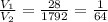
The ratio of the sides is given as
![(R_1)/(R_2)=3\sqrt[]{(1)/(64)}=(1)/(4)](https://img.qammunity.org/2023/formulas/mathematics/college/iij79ks9gs1ibub3av9abe74gbpe78r9jh.png)
Therefore, the ratio of the surface areas is given as

Therefore, the ratio is 1:16.