Question

Write the first four terms of the geometric sequence, given two terms in the sequence. If your term is not an integer type it as a decimal rounded to the nearest tenth.a_6= 25 and a_8=6.25a_1=Answera_2=Answera_3=Answera_4=Answer

Answer 1

The first four terms of the geometric sequence are;

a_{1} = 800

a_{2} = 400

a_{3} = 200

a_{4} = 100

What is the first four terms of the geometric sequence?

`a_(6) = 25`

`a_(8) = 6.25`

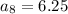
Also,

`a_(6) = {ar}^(5)`

`a_(8) = {ar}^(7)`

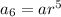
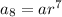
To find the common ratio, divide the 8th term by the 6th term

`\frac{{ar}^(7)}{{ar}^(5)} = (6.25)/(25)`

`{r}^(2) = 0.2`

`r = √(0.25)`

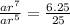
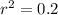
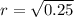
r = 0.5

The first term, a

`a_(6) = {ar}^(5)`

`25= {a * 0.5}^(5)`

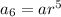
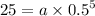
25 = a × 0.03125

25 = 0.03125a

a = 25 / 0.03125

a = 800

Second term;

ar = 800 × 0.5

ar = 400

ar² = 800 × 0.5²

= 200

ar³ = 800 × 0.5³

= 100

Answer 2

Given that:

`a_6=25\text{ and }a_8=6.25`

The general term of a geometric series with first term 'a' and common ratio 'r' is

`a_n=ar^(n-1)`

So,

`ar^5=25\text{ and }ar^7=6.25`

Divide them.

`\begin{gathered} (ar^7)/(ar^5)=(6.25)/(25) \\ r^2=0.25 \\ r=\pm0.5 \end{gathered}`

Find a.

If r = 0.5,

`\begin{gathered} a\cdot(0.5)^5=25 \\ a=800 \end{gathered}`

If r = -0.5,

`\begin{gathered} a\cdot(-0.5)^5=25 \\ a=-800 \end{gathered}`

The first four terms of the geometric sequence with a = 800 and r = 0.5 are

`\begin{gathered} a,ar,ar^2,ar^3=800,800\cdot(0.5),800\cdot(0.5)^2,800\cdot(0.5)^3 \\ =800,400,200,100 \end{gathered}`

The first four terms of the geometric sequence with a = -800 and r = -0.5 are

`\begin{gathered} a,ar,ar^2,ar^3=-800,-800\cdot(-0.5),-800\cdot(-0.5)^2,-800\cdot(-0.5)^3 \\ =-800,400,-200,100 \end{gathered}`