For this problem, we are given a certain equation, and we need to solve it over the interval [0º, 360º).
The equation is:
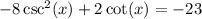
We can represent the csc as a cot, as shown below:
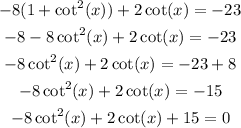
Now we can use an auxiliary variable, "y", such as:
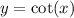
And we can rewrite the expression as:
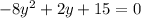
We can solve for "y", such as:
![\begin{gathered} y_(1,2)=\frac{-2\pm\sqrt[]{(2)^2-4\cdot(-8)\cdot(15)}}{2\cdot(-8)} \\ y_(1,2)=\frac{-2\pm\sqrt[]{484}}{-16} \\ y_(1,2)=(-2\pm22)/(-16) \\ y_1=(-2-22)/(-16)=1.5 \\ y_2=(-2+22)/(-16)=-1.25 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7fst0yksx9u8sgym4is9rt9af0ztl6vkcs.png)
We have two possible values for "y", and we need to solve the auxiliary equation to determine the solutions:
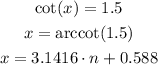
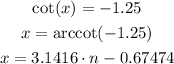
Since the cosecant is odd, we also have:
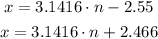
Since we want the values for x between 0 and 360º, which would be the same as 0 and 2pi rad, we have:
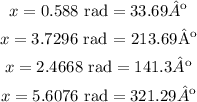
The solutions are: 33.69º, 213.69º, 141.3º and 321.29º