As the function is already given as a product, we do not need to factorize it, which is the first step to find the zeros of a function.
Now, remember that to find the zeros (also known as roots) we need to make the expression equal to 0:
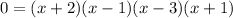
Think about this, for the function to be equal to 0 at least one of the factors must be 0, use this information to find the zeros of the function, equal each of the factors to 0 and solve for x:
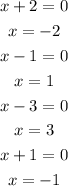
It means that the zeros of the function are -2, -1, 1, 3.
The correct answer is C.