Question

the volume of a rectangular prism is (100x¹⁸y¹²z²). if the length of the prism is (4x²y²) and the width is (5x⁸y⁷z-²), find the height of the prism.

Answer 1

We have the following rectangular prism,:

Given that we know the value of the volume, we can find the height using the following formula:

`\begin{gathered} V=a\cdot b\cdot h \\ V=100x^8y^(12)z^2 \\ a=4x^2y^2 \\ b=5x^8y^7z^(-2) \\ \Rightarrow100x^{8^{}}y^(12)z^2=(4x^2y^2)(5x^8y^7z^(-2))\cdot h \end{gathered}`

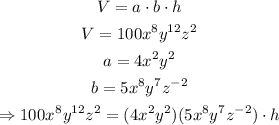
Now we multiply both factors using the rules of exponents to get the following:

`\begin{gathered} 100x^8y^(12)z^2=(4x^2y^2)(5x^8y^7z^(-2))\cdot h=(20x^(8+2)y^(2+7)z^(-2))\cdot h \\ \Rightarrow100x^{8^{}}y^(12)z^2=(20x^(10)y^9z^(-2))\cdot h \end{gathered}`

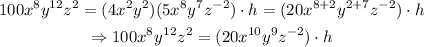
finally, we solve for h and again we use the rules of exponents on the resulting division:

`\begin{gathered} h=(100x^8y^(12)z^2)/(20x^(10)y^9z^(-2))=5x^(8-10)y^(12-9)z^(2-(-2)) \\ h=5x^(-2)y^3z^4 \end{gathered}`

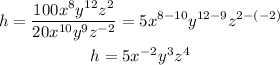
therefore, the height of the prism is h=5x^(-2)y^3z^4