Question

I have a calculus practice problem that I need help with.

Answer 1

First of all let's recal some properties of logarithmic functions:

`\begin{gathered} (1)\text{ }\log _a(b\cdot c)=\log _ab+\log _ac \\ (2)\text{ }\log _a((b)/(c))=\log _ab-\log _ac \\ (3)\log _a(b^c)=c\cdot\log _ab \end{gathered}`

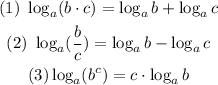
So now that we have this properties in mind let's take a look at each of the three statements given.

First we have:

`\log _3(cd^4)`

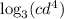
Here we can use property (1) since we have a multiplication inside the logarithm:

`\log _3(cd^4)=\log _3\lbrack(c)\cdot(d^4)\rbrack=\log _3(c)+\log _3(d^4)`

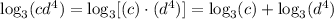
Then we can use property (3) in the second term:

`\log _3(cd^4)=\log _3(c)+\log _3(d^4)=\log _3(c)+4\log _3(d)`

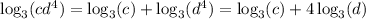
But this last expression is different than the one in the statement:

`\log _3(c)+4\log _3(d)\\e4\log _3(c)+4\log _3(d)`

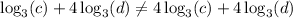
Then the first statement is False.

In the second statement we have:

`(3)/(4)(\ln a+\ln b)=\ln (\sqrt[4]{a^3b^3})`

Let's take the expression inside parenthesis at the left side and use property (1):

`(3)/(4)(\ln a+\ln b)=(3)/(4)\ln (ab)`

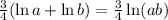
We can use property (3) in this last expression:

`(3)/(4)\ln (ab)=\ln \lbrack(ab)^{(3)/(4)}\rbrack`

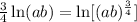
Here is important to recal some properties of powers:

`\begin{gathered} (i)\text{ }A^{(B)/(C)}=A^{B\cdot(1)/(C)}=(A^B)^{(1)/(C)} \\ (ii)\text{ }A^{(1)/(B)}=\sqrt[B]{A} \end{gathered}`

So if we use property (i):

`\ln \lbrack(ab)^{(3)/(4)}\rbrack=\ln \lbrack(a^3b^3)^{(1)/(4)}\rbrack`

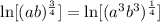
And using property (ii) we get:

`\ln \lbrack(a^3b^3)^{(1)/(4)}\rbrack)=\ln \sqrt[4]{a^3b^3}`

Which means that:

`(3)/(4)(\ln a+\ln b)=\ln \sqrt[4]{a^3b^3}`

Then the second statement is True.

The third statement is:

`3\ln e-2\ln f=\ln ((e^3)/(f^3))`

Let's take the expression in the left and use property (3) in both terms:

`3\ln e-2\ln f=\ln e^3-\ln f^2`

Now we use property (2):

`3\ln e-2\ln f=\ln e^3-\ln f^2=\ln ((e^3)/(f^2))`

Which proves that the third statement is True.