Question

Suppose that f(x) = -8x^2 + 8.(A) Find the slope of the line tangent to f(a) at x = 5.(B) Find the instantaneous rate of change of f(x) at x = 5.(C) Find the equation of the line tangent to f(a) at x = 5. Y=

Answer 1

The slope of the line tangent to f(x) at x=5 can be found through:

`m_(\tan )=\lim _(h\to0)(f(x_0+h)-f(x_0))/(h)`

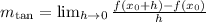
this is the same definition as the derivative of the function

then,

`\begin{gathered} f^(\prime)(x)=2\cdot-8x \\ f^(\prime)(x)=-16x \end{gathered}`

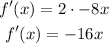
then, evaluate at the given point

`\begin{gathered} f^(\prime)(5)=-16\cdot5 \\ f^(\prime)(5)=-80 \end{gathered}`

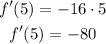
the slope of the line tangent to f(x) at x=5 is -80.

Also, we know that the instantaneous rate of change is the slope of the tangent line, meaning the instantaneous rate of change is -80 as well.

The equation of the tangent line is given by

`y-y_0=m\cdot(x-x_0)`

then, find f(5)

`\begin{gathered} f(5)=-8\cdot(5)^2+8 \\ f(5)=-200+8 \\ f(5)=-192 \end{gathered}`

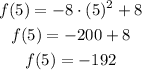
the equation of the line is

`\begin{gathered} y-(-192)=-80(x-5) \\ y+192=-80x+400 \\ y=-80x+400-192 \\ y=-80x+208 \end{gathered}`