Question

Graphing Sine & Cosine FunctionsCan you help me find the midline, amplitude, period, and phase shift? As well as graph it?

Answer 1

To answer this question we need to remember that in a function of the form:

`y=A\sin (B(\theta+C))+D`

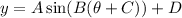
we have that:

• The amplitude is A

,

• The period is

`(2\pi)/(B)`

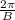
• The phase shift is C (here if C>0 the shift is to the left, otherwise is to the right).

,

• The midline is

`y=D`

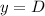
Now that we know this we need to determine the values of each constant, comparing the function given by the general expression above we have:

`\begin{gathered} A=2 \\ B=1 \\ C=-\pi \\ D=1 \end{gathered}`

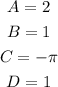
Using the definitions given above we have that:

`\text{Midline }y=1`

`\text{Amplitude 2}`
`\text{ Period }2\pi`
`\text{ Phase shift }-\pi`

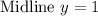
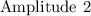
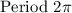
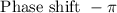
The graph of the function is: