In order to calculate the remainder of this division, we can use the remainder theorem.
This theorem states that when dividing p(x) by q(x), and q(x) has a zero x = k, the remainder of the division is given by r = p(k).
Since the division is by the polynomial x - 1 and its zero is x = 1, let's calculate the value of p(1), which will be the remainder of the division:
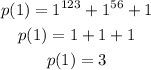
Therefore the remainder of the division is 3.