Let's compute h'(t) to find its maximum:
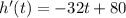
In order to find its maximum, we equal it to 0, solve for t and replace the value we get in h(t):
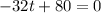
From this
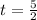
Substituting in h(t) we get:
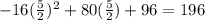
Thus the maximum height of the ball will be 196 feet.
In order to know how many seconds will pass until the ball hits the ground, we must solve h(t)=0
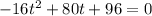
From this we get:
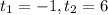
Since it doesn't make sense for the ball to hit the ground in negatve time, the ball will hit the ground after 6 seconds.