Question

A wind turbine has blades 10 meters long and a tower 38 meters high. The turbine rotates at a rate of 2 radians every 3 seconds.One of the turbine's blades is in the 3 o'clock position the instant the turbine begins moving. Define a function f that gives the distance of this blade's tip above the ground (in meters) as a function of t, the number of seconds that have passed since the turbine began moving. Determine algebraically the number of seconds that have passed during the turbine's first revolution that the tip of the blade will be 40 m above the ground. (Round your answers to four decimal places. Separate multiple solutions with a comma.)

Answer 1

As in previous analysis, the main key of this point is to analyze the circle, this looks as follows

the tip of the blade is located over the circle. We are interested on the y-coordinate of the tip of the blade. So, imagine that there is some angle between the initial position and the actual position at any time

Then, in this case, the position of the tip of the blade is determined as

`(r\cos (\theta),r\sin (\theta))\text{ }`

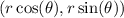
where r is the radius of the circle. In this case, r=10. So the expression would be

`(10\cos (\theta),10\sin (\theta))`

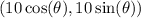
So, in this case, the y-coordinate would be

`10\sin (\theta)`

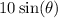
this analysis assumes that the center of the circle is at height 0. Since the center of the circle is at height 38, then if we add 38 m we would get the expression of the tip of the blade. So we get

`10\cdot\sin (\theta)+38`

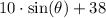
Now, we have to find the expression for theta at any time. The key is to use the rate as the blade rotates, and multiply it by the time. As an examples, suppose that 3 seconds have passed. So the angle would be

`(2)/(3)\cdot3=2`

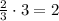
So, in general, after t seconds, the angle would be

`(2)/(3)\cdot t`

So we replace this expression for theta

`10\cdot\sin ((2)/(3)\cdot t)+38`

Now, we want to find how much time has passed so the height is 40. So we make this expression equal to 40.

`10\cdot\sin ((2)/(3)\cdot t)+38=40`

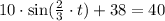
Then, we subtract 38 on both sides, so we get

`10\cdot\sin ((2)/(3)\cdot t)=40\text{ -38=2}`

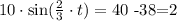
Now, we divide both sides by 10, so we get

`\sin ((2)/(3)\cdot t)=(2)/(10)=(1)/(5)`

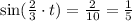
Now, we apply the inverse sine function. So we get

`\sin ^(-1)((2)/(3)\cdot t)=(2)/(3)\cdot t=\sin ^(-1)((1)/(5))=0.20135`

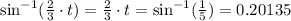
Now, we multiply both sides by 3 and divide it by 2, so we get

`t=0.20135\cdot(3)/(2)=0.30203`

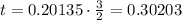
So after 0.30203 the height is 40 meters.