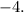Question

How to write an equation of a line that goes through the points (4, -8) and (-7, 3). I know how to find the slope but not the y-intercept.

Answer 1

To determine the equation of a line that passes through two given points (x₁,y₁), and (x₂,y₂), we can use the following formula:

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1).`

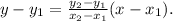
Substituting:

`\begin{gathered} (x_1,y_1)=(4,-8), \\ (x_2,y_2)=(-7,3) \end{gathered}`

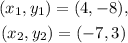
in the above formula, we get:

`y-(-8)=(3-(-8))/(-7-4)(x-4).`

Simplifying the above result, we get:

`\begin{gathered} y+8=(11)/(-11)(x-4), \\ y+8=-1(x-4), \\ y+8=-x+4. \end{gathered}`

Finally, to determine the y-intercept we can take the above equation to its slope-intercept form (y=mx+b):

`\begin{gathered} y=-x+4-8, \\ y=-x-4. \end{gathered}`

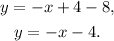
Answer:

Equation:

`y=-x-4.`

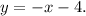
y-intercept:

`-4.`