We have the sequence 3, 6, 9, 12.
We can prove that this sequence is not geometric by calculating the ratios a2/a1 and compare it to a3/a2. If the ratios are not equal, the sequence is not geometric: there is no common ratio in the sequence.
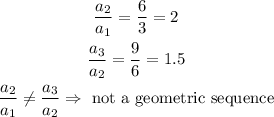
We can prove it is a arithmetic sequence because it has a common difference d=3 between consecutive terms:
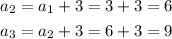
Now, we have to calculate the sum.
We start by calculating a10, using the explicit function for an arithmetic sequence:
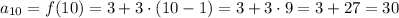
Then, we apply the formula given for the sum of n terms:
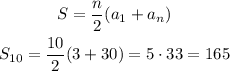
Answer:
The sequence is arithmetic.
The sum of the first 10 terms is S10=165.