We have two types of coffee:
• City roast (lets call it C), with a cost of $7.00 per pound.
,
• French roast (lets call it F), with a cost of $7.80 per pound.
They make a 8-pound blend, so the sum of the pounds of each coffee is equal to 8 pounds. We can express it as:
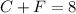
where C: pounds of City roast, and F: pounds of French roast.
The blend should cost $7.10 per pound.
The total cost of the blend is then 8*7.10 = $ 56.8.
This has to be equal to the sum of the price of City roast coffee times the quantity, 7.00*C, and the price of French roast coffe times the quantity, 7.80*F.
We can express this as:
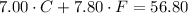
We have a system of equations with two unknowns: C and F.
We can use the first equation to express C in function of F:
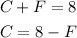
Now, we replace C in the second equation and solve for F:

Then, C can be found as:
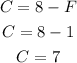
Answer:
They should buy 7 pounds of City roast and 1 pound of French roast per 8-pound blend.