Question

Determine the measure of angle ECB.Question options:1) 176.5°2) 91.75°3) 88.25°4) 183.5°

Answer 1

When we have a quadrilateral inscribed in a circle, we can use the Inscreibed Quadrilateral Theorem to infere about opposite angles of this quadrilateral.

The theorem says that the sum of opposite angles of a quadrilateral inscribed in a circle will always be 180°.

In this case, we have that:

`\angle C+\angle D=180\degree`

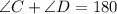
Because they are opposite angles of a quadrilateral inscribed in a circle.

Thus, let's substitute its expressions and solve for x:

`\begin{gathered} 7x+20+9x-4=180 \\ 16x+16=180 \\ 16x=164 \\ x=(164)/(16)=(41)/(4) \end{gathered}`

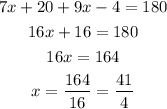
Now, to calculate the angle ECB, we can substitute x into the expression for the angle ECB:

`\angle ECB=7x+20=7\cdot(41)/(4)+20=71.75+20=91.75`

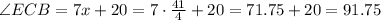
Thus, the angle ECB is 91.75°, alternative 2.