Question

the area of a circle is represented by the equation A=πR², where r is the radius. The area is 64π M². what is the length of the diameter?

Answer 1

We know that the area of the circle can be calculated using the formula:

`A=\pi r^2`

If we know that a certain circle has an area equal to 64π m², we can determine the radius of the circle as follows:

-First, replace the formula with the known area:

`\begin{gathered} A=\pi r^2 \\ 64\pi=\pi r^2 \end{gathered}`

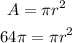
-Second, divide both sides of the equation by π:

`\begin{gathered} (64\pi)/(\pi)=(\pi r^2)/(\pi) \\ 64=r^2 \end{gathered}`

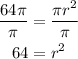
-Third, apply the square root to both sides of the equal sign to determine the length of the radius:

`\begin{gathered} \sqrt[]{64}=\sqrt[]{r^2} \\ 8=r \end{gathered}`

The radius of the circle is r=8m

The diameter of any circle is twice the radius, so that: