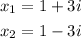Question

Hello, may I ask how to find the imaginary solutions to this problem

Answer 1

Hello!

We have the equation:

`(1)/(2)x^2-x+5=0`

Let's solve it by the method of completing the square:

I will put the unknowns on one side and the value on the other, look:

`(1)/(2)x^2-x=-5`

To remove the fraction, we can divide both sides by 1/2, obtaining:

`x^2-2x=-10`

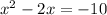
Now let's leave space to complete the square:

`x^2-2x+\square=-10+\square`

The value that will be added must be the same on both sides.

Remember we want to complete a square, so, let's write this expression as a product of factors:

`x^2-2\cdot x\cdot1+\square^2`

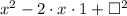
Let's replace where is the square by 1 and solve this expression:

`\begin{gathered} x^2-2\cdot x\cdot1+1^2 \\ (x^2-2x+1)\text{ we can write it as} \\ \mleft(x-1\mright)^2 \end{gathered}`

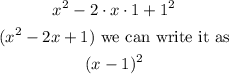
Notice that we can get a square on the left side when we use 1. So let's replace the square on the right side with 1 as well:

`\begin{gathered} (x-1)^2=-10+\square \\ (x-1)^2=-10+1 \\ (x-1)^2=-9 \end{gathered}`

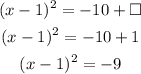
To solve this expression, we can apply the square root of both sides:

`\begin{gathered} \sqrt[]{(x-1)^2}=\sqrt[]{-9} \\ x-1=\sqrt[]{-9} \end{gathered}`

Now that the imaginary numbers part comes in, the square root of a negative number just exists in the imaginary numbers.

Let's calculate the square root of -9:

Remember that √9 = +3 or-3.

In the same way, to calculate the square root of a negative number we will follow the same steps and then replace the result with "i", in reference to imaginary numbers.

Knowing it let's finish your exercise:

`\begin{gathered} x-1=\pm\sqrt[]{-9} \\ x-1=\pm3i \\ x=+1\pm3i \end{gathered}`

As we can have a positive and a negative result, let's divide it into two results:

`\begin{gathered} x_1=1+3i \\ x_2=1-3i \end{gathered}`