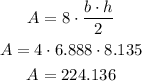Question

Find the perimeter and area of the regular polygon. rounding to three decimal places

Answer 1

This figure is a regular polygon of 8 sides.

The first step is to find the interior angle of this polygon, using the formula:

`a_i=((n-2)\cdot180)/(n)_{}`

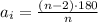
Where n is the number of vertices of the polygon. So, using n = 8, we have:

`a_i=(6\cdot180)/(8)=135\degree`

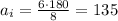
So the interior angle of a regular octagon is 135°. The segment that connects one vertex and the center of the figure divide these interior angles in 2 equal angles, so we have small isosceles triangles with base angle equal to 67.5°.

In order to find the base and height of this small triangle, we can do the following:

`\begin{gathered} \cos (67.5\degree)=((b)/(2))/(9) \\ 0.38268=(b)/(18) \\ b=6.888 \\ \\ \sin (67.5\degree)=(h)/(9) \\ \text{0}.92388=(h)/(9) \\ h=8.135 \end{gathered}`

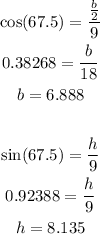
The perimeter of the octagon is:

`P=8b=8\cdot6.888=55.104`

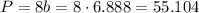
And the area is:

`\begin{gathered} A=8\cdot(b\cdot h)/(2) \\ A=4\cdot6.888\cdot8.135 \\ A=224.136 \end{gathered}`