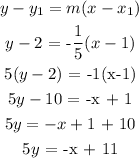Question

find the equation of the line that contains the given point and is perpendicular to the given line. (1,2),y=5×+2

Answer 1

`5y\text{ = -x + 11}`

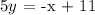
Step-by-step explanation:

Mathematically, the equation of a straight line can be represented as:

`y\text{ = mx + b}`

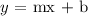
where m is the slope of the line and b is the y-intercept of the line

When two lines are perpendicular, the product of their slope values equal to -1

From the given line, it has a slope of 5

So the slope of the line perpendicular to it will be:

`\begin{gathered} m_2*\text{ 5 = -1} \\ m_2\text{ = }(-1)/(5) \end{gathered}`

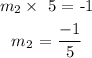
Since we have a point on the given line, we can get the equation of the said line

`\begin{gathered} y-y_1=m(x-x_1) \\ y-2\text{ = -}(1)/(5)(x-1) \\ 5(y-2)\text{ = -1(x-1)} \\ 5y-10\text{ = -x + 1} \\ 5y=-x+1\text{ + 10} \\ 5y\text{ = -x + 11} \end{gathered}`