Slope m is calculated as "rise over run" (change in y divided by change in x).
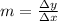
In this case, the slope is given by change in Elevation (ΔE) over change in time (Δt).
Δt is given by:
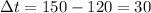
and
ΔE is given by:
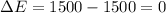
Therefore, the slope between 120 and 150 is given by:

Hence the slope of the graph between 120 and 150 minutes is 0 ft/min.
This means that between 120 and 150 minutes, there is no change in elevation.
Upslope hike is between time 0min and 120min.
Choose the two points (30min, 600ft) and (90min, 1200ft).
The slope using these two points is given by:
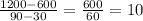
The result confirms Emma's work
The descent is between 150min and 180min.
The slope between this time period is given by:
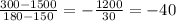
The slope during descent is -40 ft/min. The slope during descent tells us that the elevation decreases be 40ft every minute of descent.
.