Question

Find a polynomial function P(x) having leading coefficient 1, least possible degree, real coefficients, and the given zeroes -11 and 2

Answer 1

Given:

The zeroes of the polynomial are -11 and 2.

The objective is to find a polynomial function P(x) with leading coefficient 1, least possible degree.

Consider the given zeroes as, x=-11 and x=2.

Now the zeroes can be written as,

`(x+11)(x-2)=0`

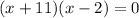
Now, multiply the terms using algebraic identitites,

`\begin{gathered} x^2-2x+11x-22=0 \\ x^2+9x-22=0 \end{gathered}`

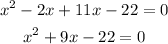
Here, the leading coefficient is 1. The real coefficients are 1, 9, -22.

Hence, the required polynomial is obtained.