Question

Simplify the expression. Write your answer as a power.(-6.1)¹¹/(-6.1)⁷ * (-6.1)²The simplified expression is __.

Answer 1

`(-6.1)^2`

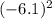
Step-by-step explanation

We are given the expression:

`\frac{(-6.1)^(11)}{(-6.1)^7\cdot\text{ }\mleft(-6.1\mright)^2}`

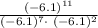
Since each of the terms have the same base (-6.1), we will simplify this by applying the law of indices.

When two terms have the same base but different powers:

=> If they are multiplying one another, we add the powers;

=> If one divides the other, subtract the power of the denominator from the numerator.

That is:

`\begin{gathered} ((-6.1)^(11))/((-6.1)^7\cdot(-6.1)^2)\text{ = }\frac{(-6.1)^(11)}{(-6.1)^{7\text{ + 2}}} \\ \Rightarrow\text{ }((-6.1)^(11))/((-6.1)^9) \\ \Rightarrow(-6.1)^{11\text{ - 9}} \\ \Rightarrow(-6.1)^2 \end{gathered}`

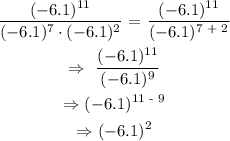
That is the simplified expression.