Hello there. To solve this question, we'll have to remember some properties about changing bases in logarithms.
Given the logarithm:
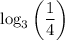
We first use the properties:
![\begin{gathered} \log_c\left((a)/(b)\right)=\log_c(a)-\log_c(b)\text{ and } \\ \\ \log_c(1)=0,0In this case, we get:<p></p>[tex]\begin{gathered} \log_3\left((1)/(4)\right)=\log_3(1)-\log_3(4)=0-\log_3(4) \\ \\ \Rightarrow-\log_3(4) \end{gathered}]()
Now, we use the change of basis formula:

When changing for a basis d greater than zero and not equal to 1.
With this, we have that
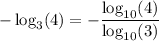
Applying the property:
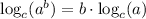
and knowing that 4 = 2², we get
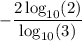
We chose base 10 log because we know the following values for:
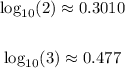
Hence the approximation for what we want is
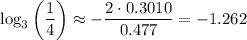
This is the answer we're looking for.