Question

Use the change of base formula to compute log314.Round your answer to the nearest thousandth.

Answer 1

Hello there. To solve this question, we'll have to remember some properties about changing bases in logarithms.

Given the logarithm:

`\log_3\left((1)/(4)\right)`

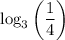
We first use the properties:

Now, we use the change of basis formula:

`\log_c(a)=(\log_d(a))/(\log_d(c))`

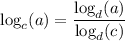
When changing for a basis d greater than zero and not equal to 1.

With this, we have that

`-\log_3(4)=-(\log_(10)(4))/(\log_(10)(3))`

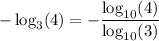
Applying the property:

`\log_c(a^b)=b\cdot\log_c(a)`

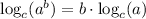
and knowing that 4 = 2², we get

`-(2\log_(10)(2))/(\log_(10)(3))`

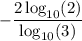
We chose base 10 log because we know the following values for:

`\begin{gathered} \log_(10)(2)\approx0.3010 \\ \\ \log_(10)(3)\approx0.477 \end{gathered}`

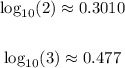
Hence the approximation for what we want is

`\log_3\left((1)/(4)\right)\approx-(2\cdot0.3010)/(0.477)=-1.262`

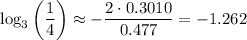
This is the answer we're looking for.