To answer this question, we can proceed as follows:
1. We can show the equations together as follows:
We can rearrange the second equation as follows:
1. Subtract 2x from both sides of the equation:
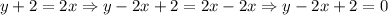
2. Subtract 2 from both sides of the equation:
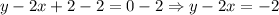
And now, we end up with the following system of equations:
We add the two equations, and then we solve for y. Now we have that the value for y = 0. If we substitute this value in either given equation, we can find the value of x as follows:
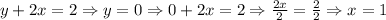
And now we have that the solution for x is 1 ( x = 1).
Therefore, the solutions for the given system is x = 1, and y = 0 or (x = 1, y = 0).
[We can double-check the result using the two given equations:
First equation

Second equation
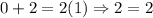
In both cases, the results are True. We have checked the result.]