Answer:
3.16 mL
Explanation:
The patient weighs 130 lb.
Since the order is for 0.15mg of drug per kilogram of body weight, convert the weight of the patient to kg.
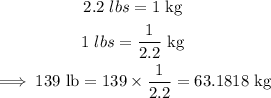
Next, determine the total mg of drug the patient requires.
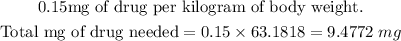
The drug label indicates the concentration to be 3mg/mL:
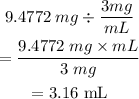
You should administer 3.16 mL of the drug (correct to 2 decimal places).