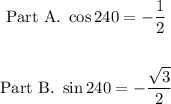Part A.
We need to find cos 240º using the cosine sum identify.
This identity is given by the formula:
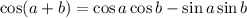
Now, we can write:
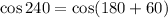
Then, we obtain:
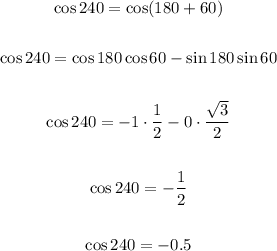
Part B.
We need to find sin 240º using the sine difference identity.
This identity is given by:
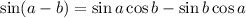
We can write:
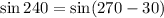
Then, we obtain:
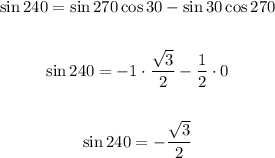
Answers