Question

two trains leave towns 1120 kilometers apart at the same time and travel toward each other.One train travels 20 km/h faster than the other.If than meet in 5 hours, what is the rate of each train.rate of the faster train:___ km/hRate of the slower train:___km/h

Answer 1

Given:

Distance between towns = 1120 kilometers

Time both trains meet = 5 hours

One train is 20 km/h faster than the other

Let's find the rate of both trains.

Let x represent the rate of the slower train.

Thus, since x represents the rate of the slower train, the rate of the faster train is:

x + 20

We have the equation that represents this situation below:

5x + 5(x + 20) = 1120

Let's solve for x.

5x + 5(x) + 5(20) = 1120

5x + 5x + 100 = 1120

Combine like terms:

10x + 100 = 1120

Subtract 100 from both sides:

10x + 100 - 100 = 1120 - 100

10x = 1020

Divide both sides by 10:

`\begin{gathered} (10x)/(10)=(1020)/(10) \\ \\ x=102 \end{gathered}`

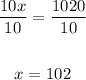
Therefore, the rate of the slower train is 102 km/h

Since the rate of the faster train is = x + 20, to find the exact rate substitute 102 for x and evaluate.

We have:

x + 20 = 102 + 20 = 122

The rate of the faster train is 122 km/h

ANSWER:

Rate of the faster train: 122 km/h

Rate of the slower train: 102 km/h