Given:
• m1 = 2.70 kg
,
• m2 = 2.30 kg
,
• m3 = 4.50 kg
,
• m4 = 1.90 kg
,
• Vertical distance = 6.00 m
,
• Horizontal distance = 4.00 m
Let's solve for the following:
• (a). Find the moment of inertia of the system about the X-axis.
To find the moment of inertia about the X-axis, apply the formula:
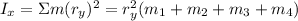
Where:
ry = 6.00/2 = 3.00 m
Thus, we have:
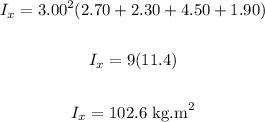
The moment of inertia about the x-axis is 102.6 kg.m².
• (b). Find the moment of inertia of the system about the Y-axis.
Apply the formula:
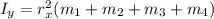
Where:
rx = 4.00/2 = 2.00 m
We have:
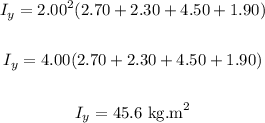
The moment of inertia about the y-axis is 45.6 kg.m².
• (c). Find the moment of inertia of the system about an axis through O and perpendicular to the page.
Apply the Perpendicular Axis Theorem.
We have:
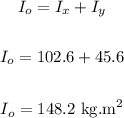
ANSWER:
• (a). 102.6 kg.m².
,
• (b). 45.6 kg.m².
,
• (c). 148.2 kg.m².