The points on a unit circle are the points (x,y) such that:
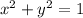
Where x and y are real numbers.
The following illustrates the unit circle:
The point P(x,y) is shown on the unit circle.
Notice that a right triangle with legs of lengths x and y and hypotenuse of length 1 (signifies the radius).
Recall the trigonometry ratio:

Substitute the length of the opposite side (y) and the length of the hypotenuse (1) into the ratio:
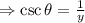
Hence, the correct answer is option C.