Question

1) Which pair of lines are parallel? Using the measurements of a given pair of angles,state a Theorem that supports your choice 2) Determine the measurements of angles x,y, and zM

Answer 1

Part 1

For this part of the exercise, we can use the Alternate Exterior Angles Converse theorem, which says that if two lines are cut by a transversal so the alternate exterior angles are congruent, then the lines are parallel.

Therefore, lines C and D are parallels since the alternate exterior angles of 95° are equal.

Part 2

From the above, we know that the angles 124° and x° are alternate exterior angles. Then, we have:

`$$\boldsymbol{m\angle x=124}$$\text{\degree}`

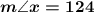
For angle y, we can use the Triangle Sum Theorem, which says that the sum of the three interior angles in a triangle is always 180°. Then, we have:

`\begin{gathered} m\angle y+53\text{\degree}+39\text{\degree}=180\text{\degree} \\ m\angle y+92\text{\degree}=180\text{\degree} \\ \text{ Subtract 92\degree from both sides of the equation} \\ m\angle y+92\text{\degree}-92\text{\degree}=180\text{\degree}-92\text{\degree} \\ $$\boldsymbol{m\angle y=88}$$\text{\degree} \end{gathered}`

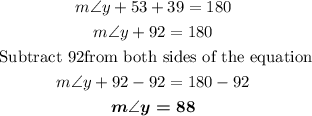
Finally, for angle z, we know that angles y and z are supplementary angles, that is, angles that add up 180°.

Then, we have:

`\begin{gathered} m\angle y+m\angle z=180\text{\degree} \\ 88\text{\degree}+m\angle z=180\text{\degree} \\ \text{ Subtract 88\degree from both sides of the equation} \\ 88\text{\degree}+m\angle z-88\text{\degree}=180\text{\degree}-88\text{\degree} \\ $$\boldsymbol{m\angle z=92}$$\text{\degree} \end{gathered}`