Question

The day that the Lord gives the speed as measured by radar of a random sample of 12 vehicles traveling on 95 calculate the first second and third quarter of the data also determine the interquartile range

Answer 1

Given the following speed in radar below,

`61,65,67,68,68,70,77,80,87,88,103,105`

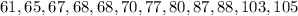
To find the first quartile, Q₁ below, where N = 12

`Q_1=((N+1)/(4))^(th)_{}=((13)/(4))^(th)=3.25^(th)`

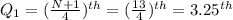
Hence, Q₁ = 68

To find the second quartile, Q₂, where N = 12,

`\begin{gathered} ^{}Q_2=\lbrack2((N+1)/(4))\rbrack^(th)=\lbrack2((12+1)/(4))\rbrack^(th)=\lbrack2((13)/(4))\rbrack^(th)=\lbrack(26)/(4)\rbrack^(th)=6.5^(th) \\ \end{gathered}`

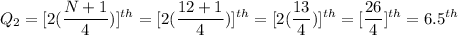
Since the median lies between the 6th and 7th data, hence Q₂ is,

`Q_2=(70+77)/(2)=(147)/(2)=73.5`

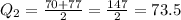
Hence, Q₂ = 73.5

To find the third quartile, Q₃, where N = 12,

`Q_3=\lbrack3((N+1)/(4))\rbrack^(th)=\lbrack3*3.25\rbrack^(th)=9.75^(th)`

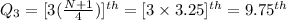
Hence, Q₃ = 88

To find the Interquartile range (IQR),

`\begin{gathered} IQR=Q_3-Q_1=88-68=20 \\ \text{IQR = 20} \end{gathered}`

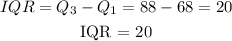
Hence, IQR = 20