Question

I've completed i (1/alpha+1/beta+1/lambda) i need some help with ii (alpha+2)(beta+2)(lambda+2)

Answer 1

The degree of an equation dictates the number of roots/number of factors an equation has. Since the degree of a cubic equation is 3, we can say that it will have 3 roots, say, α, β and γ. When an equation has 3 roots, you can also say that it has 3 factors viz, (x-α), (x-β), and (x-γ). Since these are the three factors of the equation, the product of these three will give you the cubic equation.

When these three factors are multiplied and simplified, we get,

x^3 – (α+β+γ)x^2 + (αβ + βγ + γα)x – αβγ = 0. Comparing with the standard form,

ax^3 + bx^2 + cx + d = 0, we have

Sum of roots =

`(\alpha+\beta+\gamma)=-(b)/(a)`

Product of roots =

`\alpha\beta\gamma=-(d)/(a)`

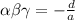
Sum of the product of roots taken two at a time

`(\alpha\beta+\beta\gamma+\gamma\alpha)=(c)/(a)`

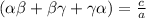
(i)

a = 1

b = - 8

c = 28

d = -32

`\begin{gathered} (1)/(\alpha)+(1)/(\beta)+(1)/(\gamma) \\ (\beta\gamma+\alpha\gamma+\alpha\beta)/(\alpha\gamma\beta) \\ (c/a)/(-d/a) \\ -(c)/(d) \\ -(28)/(-32) \\ (7)/(8) \end{gathered}`

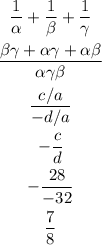
The answer of part (i) is 7/8

(ii)

`\begin{gathered} (\alpha+2)(\beta+2)(\gamma+2) \\ (\alpha\beta+2\beta+2\alpha+4)(\gamma+2) \\ (\alpha\beta\gamma+2\beta\gamma+2\alpha\gamma+4\gamma+2\alpha\beta+4\beta+4\alpha+8) \\ (\alpha\beta\gamma)+2(\beta\gamma+\alpha\beta+\alpha\gamma)+4(\alpha+\beta+\gamma)+8 \\ -(d)/(a)+(2c)/(a)-(4b)/(a)+8 \end{gathered}`

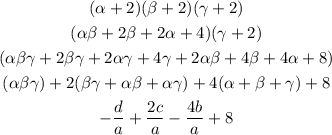
a = 1

b = - 8

c = 28

d = -32

`\begin{gathered} -(-32)/(1)+(2\cdot28)/(1)-(4\cdot-8)/(1)+8 \\ 128 \end{gathered}`

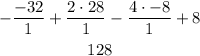
The answer of part (ii) is 128