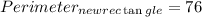
Step-by-step explanation
To find the perimeter of a rectangle, add the lengths of the rectangle's four sides.
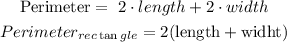
Step 1
Let
W represents the width
L represents the lengh
hence,the length of a rectangle is 3 times its width.
traslate,
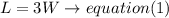
and the perimeter is 72,so

Step 2
solve the equations:
a)replace equation (1) in equation (2)
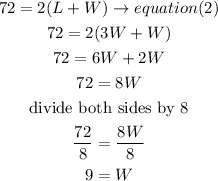
it means the width is 9 units
b)
now, replace the W value in equation (1)
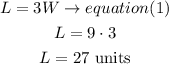
so, for the original rectangle

Step 3
now , find the new perimeter if the length were increased by 2
Let
Length= 27 units + 2 units=29 units
width=9 units
replace to find the perimeter
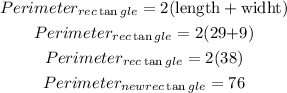
I hope this helps you