1 Answer

Hellter · Answer 1 · 2023-06-25T14:56:51+0000

The given system of equations are,

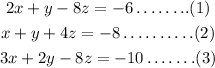
$\begin{gathered} 2x+y-8z=-6\ldots\ldots..(1) \\ x+y+4z=-8\ldots\ldots\ldots\text{.}(2) \\ 3x+2y-8z=-10\ldots\ldots\text{.}(3) \\ \\ \end{gathered}$

Substracting equation (3) from equation (1),

$\begin{gathered} (2x+y-8z)-(3x+2y-8z)=-6-(-10) \\ -x-y=4\ldots\ldots\ldots\text{.}\mathrm{}(4) \end{gathered}$

Multiplying equation (2) by 2 and adding it to equation (1),

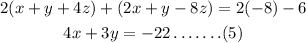
$\begin{gathered} 2(x+y+4z)+(2x+y-8z)=2(-8)-6 \\ 4x+3y=-22\ldots\ldots\text{.}(5) \end{gathered}$

Multiplying equation (4) with 4 and adding to equation (5),

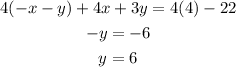
$\begin{gathered} 4(-x-y)+4x+3y=4(4)-22 \\ -y=-6 \\ y=6 \end{gathered}$

Substituting the value of y in the equation (4)

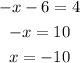
$\begin{gathered} -x-6=4 \\ -x=10 \\ x=-10 \end{gathered}$

Substituting the value of x and y in the equation (1),

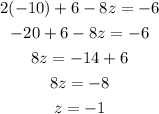
$\begin{gathered} 2(-10)+6-8z=-6 \\ -20+6-8z=-6 \\ 8z=-14+6 \\ 8z=-8 \\ z=-1 \end{gathered}$

Thus, x=-10, y=6 and z=-1 are the required value of all the three variables.

Please log in or register to add a comment.