Question

Please tell answer with steps.

Answer 1

`√(3) - (\pi)/(2)`

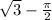
Explanation:

Firstly, you connect the three origins, and then a triangle form, the triangle is certainly an equilateral triangle.

The three sides of the triangle are all 2cm because the radius of the three coins are 1cm, it's very easy to understand.

Now, using the Pythagorean theorem (of you have a right triangle with two sides a, b and the hypotenuse c, you can see that
`\sqrt{a^(2) +b^(2) }=c`,
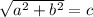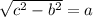`\sqrt{c^(2)-b^(2) } =a`and
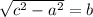`\sqrt{c^(2)-a^(2) } =b`), we can get the area of the equilateral triangle by calculating the two right triangles in it (you can get the two triangles by drawing a line connecting the point of one angle to the middle point of its opposite side)

The area of one of the two small right triangles is:
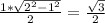`\frac{1*\sqrt{2^(2)-1^(2) }}{2}=(√(3) )/(2)`, and the sum of the area of the two right triangles, which is also the area of the equilateral triangle is:
`2*(√(3) )/(2)=√(3)`

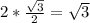
We calculate all this because we need to use the area of the equilateral triangle to subtract the area of the three sectors in it, and the result will be the area of the shaded area.

Now, to calculate the area of the three sectors, we need to know the angles of them, which is 60 degrees(because they are in an equilateral triangle). And then, the area of one of the three sectors(they are completely the same) are
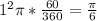`1^(2) \pi *(60)/(360) =(\pi )/(6)`, so the sum of the three sectors are
`(\pi )/(6)*3=(\pi)/(2)`.

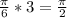Then, the shaded area of the area of the equilateral triangle subtract the area of the three sectors, which is
`√(3) -(\pi)/(2)`

If you want the result in decimals, you can use a calculator.

Hope this will help:)

P.S. Typing this rly took me a LONG time >_<