Question

jessica dale and milan served a total of 77 orders jessica served 5 more orders than dale and milan served 2 times as many as dale how many did they each serve

Answer 1

Let be "j" the number of orders that Jessica served, "d" the number of orders that Dale served and "m" the number of orders that Milan served.

Based on the information given in the exercise, you can set up the following System of equations:

`\begin{gathered} \begin{cases}j+d+m=77 \\ j=d+5 \\ m=2d\end{cases} \\ \end{gathered}`

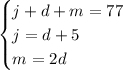
The steps to solve it are shown below:

1. Substitute the second equation and the third equation into the first one:

`\begin{gathered} j+d+m=77 \\ (d+5)+d+(2d)=77 \end{gathered}`

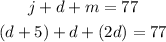
2. Solve for the variable "d":

`\begin{gathered} 4d+5=77 \\ 4d=77-5 \\ \\ d=(72)/(4) \\ \\ d=18 \end{gathered}`

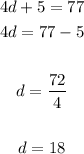
3. Substitute this value into the second original equation and evaluate:

`\begin{gathered} j=d+5 \\ j=(18)+5 \\ j=23 \end{gathered}`

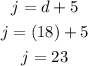
4. Substitute the value of "d" into the third equation and then evaluate:

`\begin{gathered} m=2d \\ m=2(18) \\ m=36 \end{gathered}`

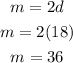
Therefore, the answer is:

- Jessica served 23 orders.

- Dale serverd 18 orders.

- Milan served 36 orders.