Question

Find the height of the building in the figure below to the nearest foot

Answer 1

Let's call the base of the smaller triangle as x and the height of the building as h.

In a right triangle, the tangent of an angle is the length of the opposite side divided by the length of the adjacent side. From this statement, for the smaller triangle we have the following relation

`\tan (48^o)=(h)/(x)`

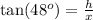
Rewritting this equation as a function for x, we have

`x=(h)/(\tan(48^o))`

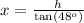
For the bigger triangle, we can use the same trigonometric relation.

`\tan (35^o)=(h)/(x+150)`

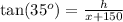
If we substitute the expression for x on this equation, we're going to have a new equation only for the height of the building

`\tan (35^o)=(h)/((h)/(\tan(48^o))+150)`

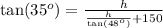
Solving for h, we have

`\begin{gathered} \tan (35^o)=(h)/((h)/(\tan(48^o))+150) \\ \tan (35^o)\cdot((h)/(\tan(48^o))+150)=(h)/((h)/(\tan(48^o))+150)\cdot((h)/(\tan(48^o))+150) \\ (\tan (35^o))/(\tan (48^o))h+150\tan (35^o)=h \\ (\tan(35^o))/(\tan(48^o))h+150\tan (35^o)-150\tan (35^o)=h-150\tan (35^o) \\ (\tan(35^o))/(\tan(48^o))h=h-150\tan (35^o) \\ (\tan(35^o))/(\tan(48^o))h-h=h-150\tan (35^o)-h \\ (\tan(35^o))/(\tan(48^o))h-h=-150\tan (35^o) \\ h((\tan(35^o))/(\tan(48^o))-1)=-150\tan (35^o) \\ (1)/(\tan(35^o))\cdot(h((\tan(35^o))/(\tan(48^o))-1))=-150\tan (35^o)\cdot(1)/(\tan(35^o)) \\ h((1)/(\tan (48^o))-(1)/(\tan(35^o)))=-150 \\ h(\cot (48^o)-\cot (35^o))=-150 \\ h=-(150)/(\cot (48^o)-\cot (35^o)) \\ h=284.22873718\ldots \\ h\approx284 \end{gathered}`