Question

I'm unsure how to determine the transformation of this graph.

Answer 1

The given graph is a graph of the absolute value function:

`y=f(x)=|x|`

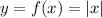
A graph of the function y=f(x) when translated horizontally by a units, vertically by b units, and horizontally stretched by a factor of k, where k>=1 is :

`y=(1)/(k)f(x-a)+b`

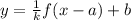
The required graph in the choices is that of the function:

`y=(1)/(3)f(x+5)-3`

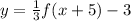
This equation shows that the new function translates the previous one vertically down by 3 units (b=-3).

Horizontally to the left by 5 units (a=-5), and a horizontal stretch by a factor of 3 (k=3).

Hence, the new graph will be the one that gives the old graph translated vertically downwards by 3 units, horizontally to the left by 5 units, and a horizontal stretch away from the y-axis by a factor of 3.

The graph that best fits is shown below: