Hello there. To solve this question, we'll have to remember some properties about determine the Z-score.
First, remember the Z-score of a raw score x, given the population mean μ and the standard deviation σ can be calculated by the following formula:
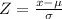
Also, remember that a Z-score is said to be unusual if it is more than 2 standard deviations away from the mean. Thinking of the distribution of the women's height as a graph:
Okay. So now we solve:
a) To find the Z-score corresponding to a women with a height of 70 inches.
Plugging x = 70, μ = 63.6 and σ = 2.5, we have:
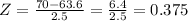
In this case, as the Z-score is something between -2 and 2, then it indicates we have an ordinary Z-score (means it is not unusual).
b) To find the Z-score corresponding to a woman with a height of 59 inches.
Plugging x = 59, μ = 63.6 and σ = 2.5, we get
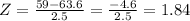
Again, since it is between -2 and 2, it is not unusual.
c) Find the height of a woman whose height is 1.5 standard deviation below the mean.
In this case, we know that Z = -1.5, such that we can plug μ = 63.6, σ = 2.5 and solve for x:
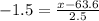
Multiply both sides of the equation by a factor 2.5
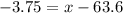
Add 63.6 on both sides of the equation
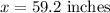
These are the answers for the questions.